Adventi naptár
Czirkos Zoltán · 2021.05.31.
Síelés
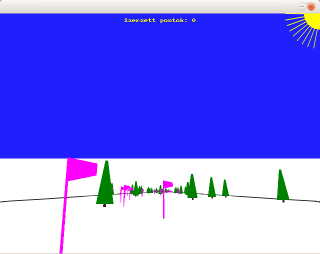
Síeljünk! Itt egy program, ami három dimenzióban rajzolja ki a sípályát. A pályán, amelynek széleit egy halvány szürke vonal jelzi, bóják és fák vannak. Természetesen lejt is. A síelő ezen halad lefelé; egy fának nekimenve pontlevonást kap, bóját eltalálva pontot. A játékban kanyarodni a balra és jobbra nyilakkal lehet; hóekézni pedig a lefelé nyíllal.
A játék érdekessége, hogy programozási szempontból alig különbözik a múltkor bemutatott repülős játéktól – ugyanazok a problémák kerülnek elő itt is (változó számú objektumok, egymás átfedése stb.), mint annál.
A játékban hősünk elvileg egy lejtős pályán száguld lefelé a fák és bóják között a
völgy felé. Az „elvileg” itt nem töltelékszó, mert ez a programban nem feltétlenül kell így
történjen: végülis nem muszáj a programban a lejtős pályát számolni, éppen elegendő az is, ha az
eredmény úgy néz ki, mintha lejtene a pálya. Sőt hősünknek nem muszáj a fák és bóják
felé csúsznia sem: az is jó, ha a fák és a bóják jönnek felé. A látvány a monitoron ugyanolyan
lesz! Induljunk ki ebből a gondolatból, mert mint kiderül, a dolgunk sokkal egyszerűbb lesz, ha a
játékos a tér origójában van.
Tehát a program dolga a következő. Minden időlépésben a pálya összes elemének z
koordinátáját csökkenti, azaz mindent a játékos felé mozgat. Ha valamelyik pályaelem a játékos
mögé kerül, akkor azt már
el lehet dobni. Hátrafordulni úgysem fog, és hegynek felfelé csúszni sem. Így egyre fogynak az
akadályok a pályán – vagyis fogynának, ha a program nem generálna véletlenszerűen újakat jó messze
a játékostól. A main() függvény ide vonatkozó része minden hosszegységenkénti
csúszás után (ami a programban tíz méter) generál néhány új pályaelemet.
Mivel az új elemek messze vannak, és a közelebbi fák eltakarják azokat, ez nem észrevehető.
(Ha az ELEMEK konstans értékét túl alacsonyra állítjuk, akkor viszont nagyon is.)
Apropó, láthatóság! Ahogyan a repülős programban meg kellett oldani, hogy a repülők felül legyenek,
és a tájképesnél is figyelni kellett a négyszögek sorrendjére, itt is foglalkozni kell ezzel a
problémával. A közeli tárgyaknak el kell fedniük a távoliakat!
Egy kis trükkel ez itt egyszerűen megoldható: mivel az egyes pályaelemek távolságviszonya,
z koordináta szerinti sorrendje nem változik, nem kell soha sorbarendezni őket. Ha
fogunk egy várakozási sort, és annak a végére kerülnek az új fák, bóják, a sor elején pedig azok
vannak, amelyek már a legközelebb vannak a játékoshoz, éppen olyan sorrendben lesznek benne az
elemek (hátulról előrefelé), ahogyan ki kell rajzolni azokat. A program láncolt listája ehhez
képest szándékosan pont fordítva van, mert akkor a láncolás sorrendje megegyezik a kirajzolás
sorrendjével. Így a lista elején a legtávolabbi elemek vannak, ezért az újakat oda
kell beszúrni; a kirajzoláshoz pedig előrefelé kell haladni a listában. Az elejére beszúrást meg
úgyis szeretjük, az a legegyszerűbb.
A main() függvény v változója tárolja a játékos sebességét és a
csúszásának irányát (szog) is. Az utóbbinál a 90 fok jelenti az egyenesen előrét,
azaz a völgy irányát. Ezekből számolódik ki az, hogy éppen hol van a pályán – de csak az x
koordináta, xpos, mivel az y mindig nulla. A játék hangulatát
és látványosságát javítandó, a doles változó azt a szöget tárolja, ahány fokkal a
játékos bedől a kanyarban. A kirajzoláskor ennyivel elforgatja a teljes nézetet. Ezen változók
kezelése az eseményhurokban történik. A dőlés 10 fokra, a mozgási irány eltérése a völgynek lefelétől
pedig 15 fokra van maximálva:
doles *= 0.7;
if (key[SDL_SCANCODE_LEFT]) { /* balra kanyarodas - nyomva tartassal */
szog -= 3;
if (szog < 75) /* limit */
szog = 75;
if (doles > -10) /* bedoles a kanyarban (z tengely szerinti forg.) */
doles -= 1;
}A doles*=0.7 értékadás hatására a gomb elengedése után rövid időn belül visszatér
egyenesbe a nézet. A mozgás lelkét az alábbi a programrész adja:
lefele += -v*sin(szog * 3.14 / 180);
/* ha ennyit ment lefele, akkor uj HOSSZEGYSEGnyi meretet general a palyahoz */
if (lefele < -HOSSZEGYSEG) {
uj_palyaresz(&lista, (ELORE - 1)*HOSSZEGYSEG);
lefele += HOSSZEGYSEG;
}
jelenet_mozgat(&lista, 0, 0, -v*sin(szog * 3.14 / 180));
jelenet_feldolgoz(hatter, &lista, xpos, (szog-90)*3.14/180, doles*3.14/180, &pont);Ez az előbb említett módon számolja, hogy mennyit csúszott lefelé a játékos, és szükség
esetén új pályaelemeket hoz létre: uj_palyaresz(). Aztán mozgatja a játékos felé
a fákat, bójákat: jelenet_mozgat(), és végül kirajzol mindent:
jelenet_feldolgoz(). A feldolgozás része az is, hogy a játékos mögé került elemek
törlődnek. Ezt azért volt kényelmes így megoldani, mert a forgatás által is kerülhetnek negatív
z koordinátára pályaelemek, a forgatás pedig a kirajzolás közben történik csak meg.
Minden egyes tárgy, amelyik a képernyőn megjelenik, először még három dimenzióban van,
x, y, és z koordinátákkal is rendelkezik. Az x tengely a vízszintes, az
y a függőleges (de felfelé nő, nem lefelé), a z tengely pedig a mélységet jelenti,
vagyis az átdöfi a monitort. A nagyobb z koordinátájú tárgyak távolabb vannak. Ezeket a
három dimenziós koordinátákat kell leképezni a két dimenziós monitorra.
Minél messzebb van egy tárgy, annál kisebbnek kell látszódjon. A drótvázas testek kirajzolása
kapcsán már szerepelt az, hogyan képezhetőek le a koordináták:
Láttuk, hogy a leképezés képlete a két háromszög hasonlóságából vezethető le, és azt is, hogy a leképezett
tárgyak alakja függ a megfigyelő vetítési síktől (itt: y tengely) vett távolságától. A síelős programban
ez tovább egyszerűsödik, ugyanis ebben a játékos nem kívülről szemléli a teret, hanem benne lesz
abban. Ahogy az előbb már szerepelt: konkrétan ő lesz az origában, tehát d=0.
Ettől a perspektívát leíró y'=d·y/(d+z)
képlet persze megbolondulna, úgyhogy tekintsünk inkább d=1-et. Írjunk bele még egy ex-has
dolgot a képletbe. Döntsük el már most, hogy a programban tárolt koordináták méterben lesznek megadva. Például
ha egy fenyőfa négy méter magas, legyen annak koordinátája y=4. Végülis mindegy, hogy milyen
arányokat választunk, ezért megtehetjük, hogy egy nekünk kényelmeset adunk meg. Hogy a képernyőn megjelenő
fenyőfa ne legyen négy pixeles, nagyítsuk fel a kapott képet. Vagyis térjünk át a játékbeli koordinátákról
(világkoordinátákról) képernyőkoordinátákra ezekkel a képletekkel:
xk = f.x/(f.z+1)*500 + kep->w/2;
yk = -f.y/(f.z+1)*500 + kep->h/2;A játékos origóba helyezése miatt a számítások nagyon leegyszerűsödnek, különösen a három
forgatás, amellyel a program számol. Ezek a következők. Először is, a világkoordináták szerint sík pályát meg
kell dönteni előrefelé, azaz
meg kell forgatni az x tengely körül (pitch). Emiatt olyan, mintha lejtene az egész.
Meg kell forgatni az y tengely körül is (yaw), mégpedig azért, mert ez adja a játékos
csúszásirányát. Végül pedig, kell egy forgatást végezni a z tengely körül (roll), mert
ebből lesz a kanyarban bedőlés. Mindezt azután, hogy a kirajzolás közben a tárgyak koordinátáit
elmozdítottuk xpos-zal, és még függőlegesen lefelé -1,7 méterrel. Miért? Mert az
a játékos szemmagassága:
f = pont3d_eltol(negyszog[i], xpos, -1.7, 0); /* sielo x pozicioja es szemmagassaga */
f = pont3d_forgat_x(f, 13*3.14/180); /* lejto dolese */
f = pont3d_forgat_y(f, irany); /* fordulas (merre nez) */
f = pont3d_forgat_z(f, doles); /* kanyarban doles */Ha a -1.7 helyett -10-et írunk, azt fogjuk látni, amit a repülős játékban
a pilóták láttak.
A perspektíva képletével a gond ott kezdődik, ha olyan pont koordinátáit helyettesítjük be, amelyek a néző
mögött vannak (vagyis z<0). Ilyen esetekre a képlet hamis eredményt ad: a negatív előjel miatt
fejjel lefelé fordítja a képet – azt a képet, amit elvileg a játékos nem is lát.
Egy félig előtte, félig mögötte lévő szakaszt nem lehet kirajzolni
egy egyszerű kétdimenziós, monitoron lévő szakaszként: annak egyik pontja helyesen számolódik, a másodikra
viszont helytelen az eredmény. A programban ezért csalni fogunk: az ilyen szakaszokat,
vagyis az ilyen sokszögeket egyszerűen eldobjuk. Előbb-utóbb minden tereptárgy mellett elhalad a síelő,
ezért az összes tárgy erre a sorsra jut.
A kirajzolt sokszögek egyébként a programban mind négyszögek. Minden tárgyhoz két négyszög tartozik, amelyek eltérő színűek lehetnek:
typedef struct Targy {
enum { fa, boja, palyaszele } tipus;
bool nekiment; /* igaz, ha mar megkapta erte a pontot */
Pont3D p0; /* referenciapont */
Pont3D n1[4], n2[4]; /* ket negyszog - rajzhoz */
Uint32 c1, c2; /* ket szin */
struct Targy *kov; /* lancolt listahoz */
} Targy;A fenyőfa háromszöge, és a bója zászlója egyszerűen úgy van megcsinálva, hogy két-két pontjuk
nagyon közel van egymáshoz. A tárgyakat létrehozó függvények a fa_hozzaad() és
boja_hozzaad(). Ezeknek egy p0 pontot lehet megadni, amelyhez képest az új
tárgyat elhelyezik. Sok a csalás megint. :) A fenyőfa például teljesen lapos, csak mindig szinte
szemből látjuk. A megadott koordináták szerint függőlegesen, pontosan felfelé nő, az y
tengely irányába. Ezzel nem is lenne gond, ha nem forgatnánk el az egész pályát az x
tengely körül egy kicsit a kirajzoláskor. Látszik is valamennyire a játék közben, hogy
ettől ferdék valamennyire. Persze a fenyőfa létrehozásánál lehetne kompenzálni, ha a csúcsához a
p0-nál valamilyen közelebbi pontot választanánk, de nem lényeges. A függvényekben
megadott koordinátákat kockás lapra lerajzolva egyébként szépen kiadódnának a rajzok. Például a
fa:
Targy *fa_hozzaad(Pont3D p0) {
Targy *uj = (Targy *) malloc(sizeof(Targy));
uj->tipus = fa;
uj->nekiment = false;
uj->p0 = p0;
uj->n1[0] = pont3d_eltol(p0, -0.1, 0, 0);
uj->n1[1] = pont3d_eltol(p0, -0.1, 0.3, 0);
uj->n1[2] = pont3d_eltol(p0, 0.1, 0.3, 0);
uj->n1[3] = pont3d_eltol(p0, 0.1, 0, 0);
uj->c1 = 0x402020FF; /* barna */
uj->n2[0] = pont3d_eltol(p0, -0.8, 0.3, 0);
uj->n2[1] = pont3d_eltol(p0, -0.1, 4.3, 0);
uj->n2[2] = pont3d_eltol(p0, 0.1, 4.3, 0);
uj->n2[3] = pont3d_eltol(p0, 0.8, 0.3, 0);
uj->c2 = 0x008000FF; /* zold */
return uj;
}
A sokszögeket az SDL fillPolygonColor() függvénye rajzolja ki. Ennek bárhány csúcsból álló
sokszöget meg lehet adni, és kifesti a belsejét is, nem csak a körvonalait rajzolja meg. A forgatások
és a szemmagasság miatti eltolási transzformáció után ellenőrizzük, hogy a forgatott pont z koordinátája
nem lett-e túl kicsi vagy negatív; ha az lett, akkor a negyszog_kepernyore() függvény
nem rajzolja ki a poligont, hanem 1-gyel tér vissza. Ezzel jelzi a hívó jelenet_feldolgoz()
függvénynek, hogy az adott tárgyat a listából el kell távolítani. Mivel a tárgyak közelednek a néző felé,
ha egyszer kicsi a z koordinátájuk, akkor már később csak még kisebb lesz.
Az utóbbi függvény végzi egyébként az ütközések ellenőrzését is, amihez a pályaelemek p0
adattagját használja.
A letölthető SDL-es program (advent20-si.c) a szokásos módon fordítható. A bemutatott trükkökkel együtt 320 kódsorba fért be a dolog.